Using mmcc with greta

Nicholas Tierney

2018-08-03

reticulate::use_virtualenv("r-tensorflow")
# ignore this ^^ for the moment
library(greta)
#> 
#> Attaching package: 'greta'
#> The following objects are masked from 'package:stats':
#> 
#>     binomial, poisson
#> The following objects are masked from 'package:base':
#> 
#>     %*%, backsolve, beta, colMeans, colSums, diag, forwardsolve,
#>     gamma, rowMeans, rowSums, sweep, tapply

# data
x <- as_data(iris$Petal.Length)
y <- as_data(iris$Sepal.Length)

# variables and priors
int <- normal(0, 1)
coef <- normal(0, 3)
sd <- student(3, 0, 1, truncation = c(0, Inf))

# operations
mean <- int + coef * x

# likelihood
distribution(y) <- normal(mean, sd)

# defining the model
m <- model(int, coef, sd)

# sampling
draws <- mcmc(m, 
              n_samples = 1000,
              chains = 4)
#> 
#> chain 1/4
#> 
#> chain 2/4
#> 
#> chain 3/4
#> 
#> chain 4/4

We can get a one-line summary of the model with glance

library(mmcc)
#> Loading required package: broom

glance(draws)
#>   n_chains n_iter n_var ess_lower ess_upper rhat_lower rhat_upper
#> 1        4   1000     3  2202.699  3119.066   1.002343   1.007604

We can also get a one-coefficient per row summary using tidy:

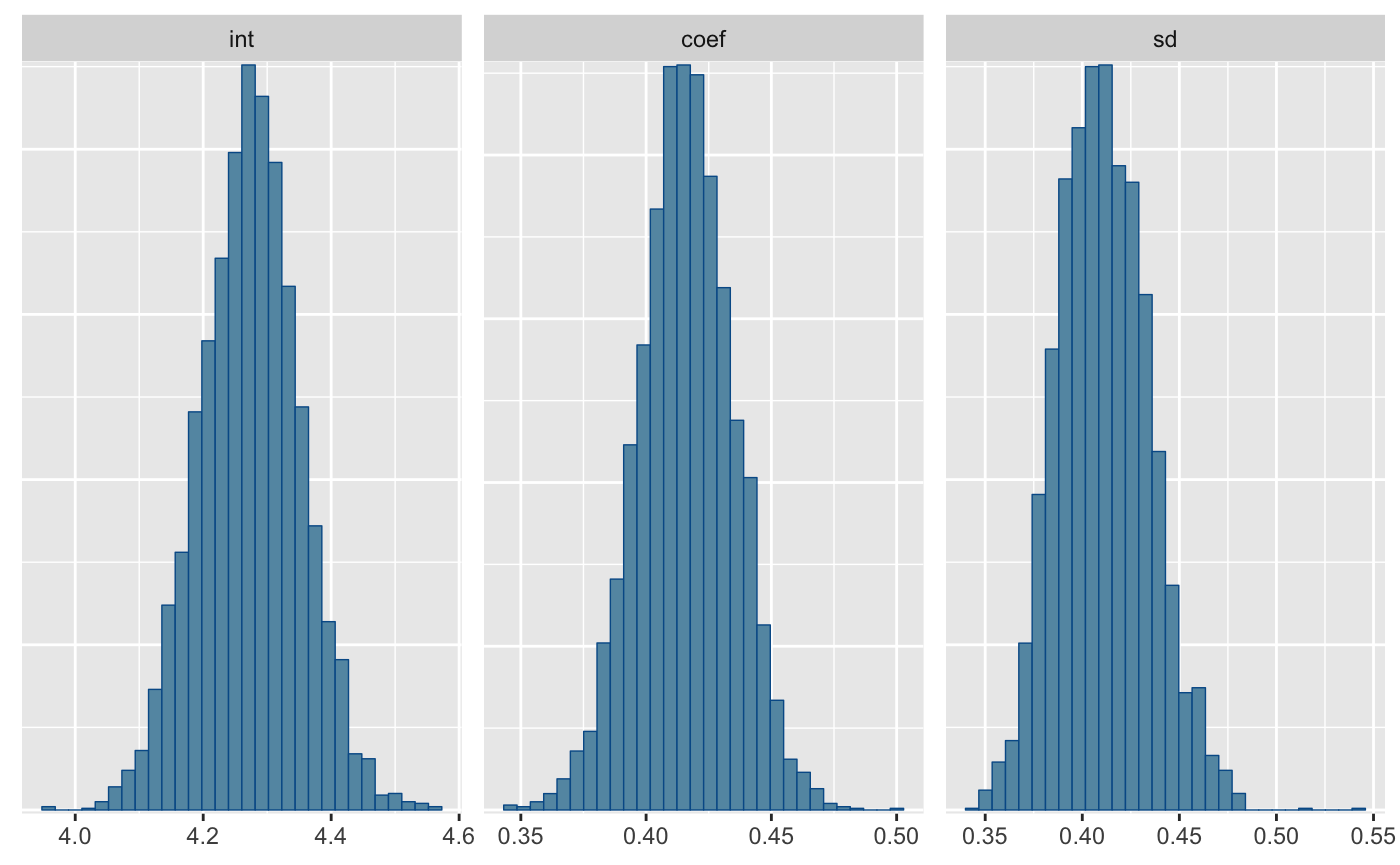
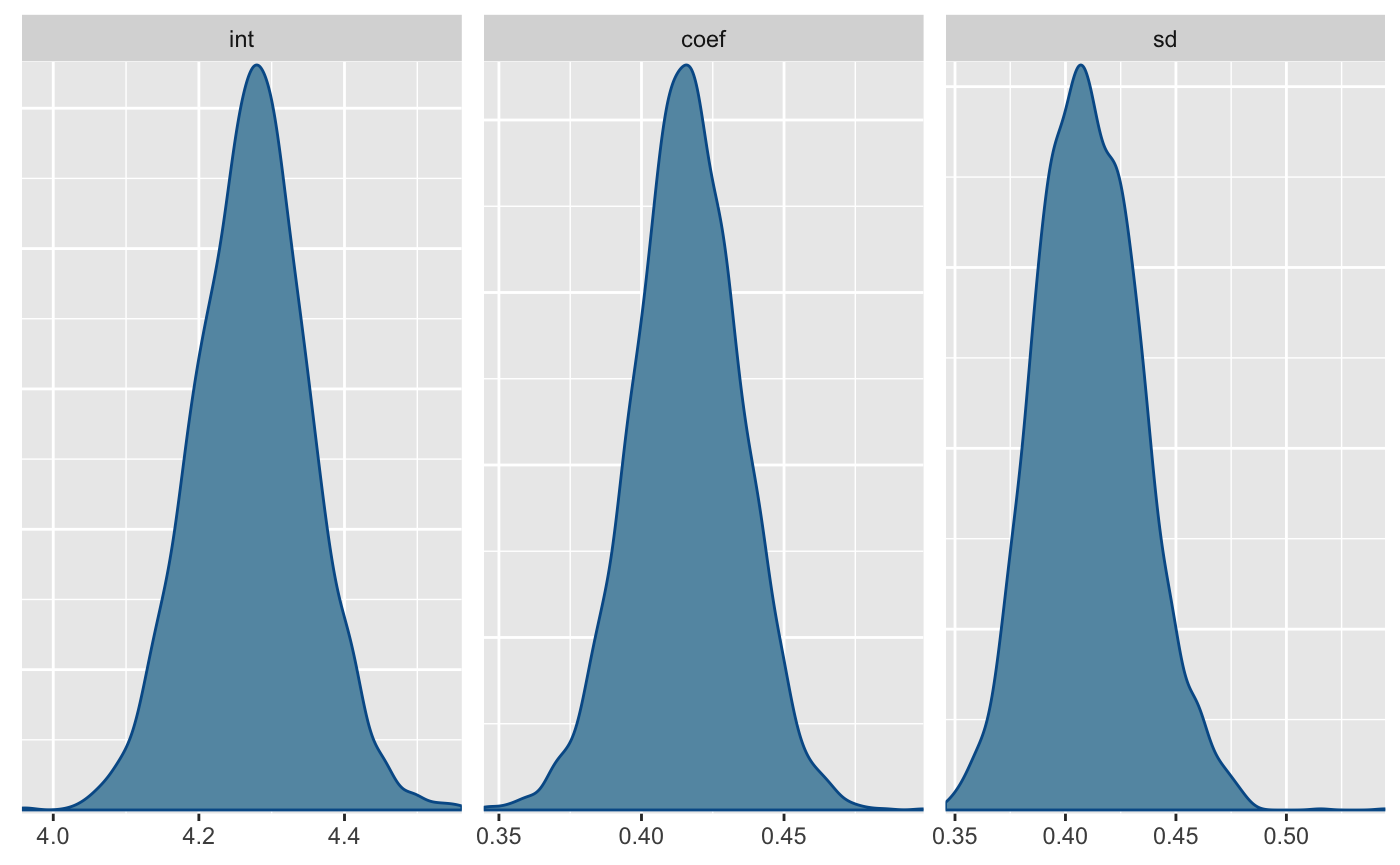
tidy(draws)
#>    parameter      mean         sd      2.5%    median     97.5%
#> 1:       int 4.2736855 0.07834333 4.1211185 4.2746592 4.4261197
#> 2:      coef 0.4159039 0.01896392 0.3784770 0.4158914 0.4522548
#> 3:        sd 0.4109504 0.02338949 0.3688096 0.4097621 0.4598336

Now we can neaten up the draws with mcmc_to_dt to facilitate plotting

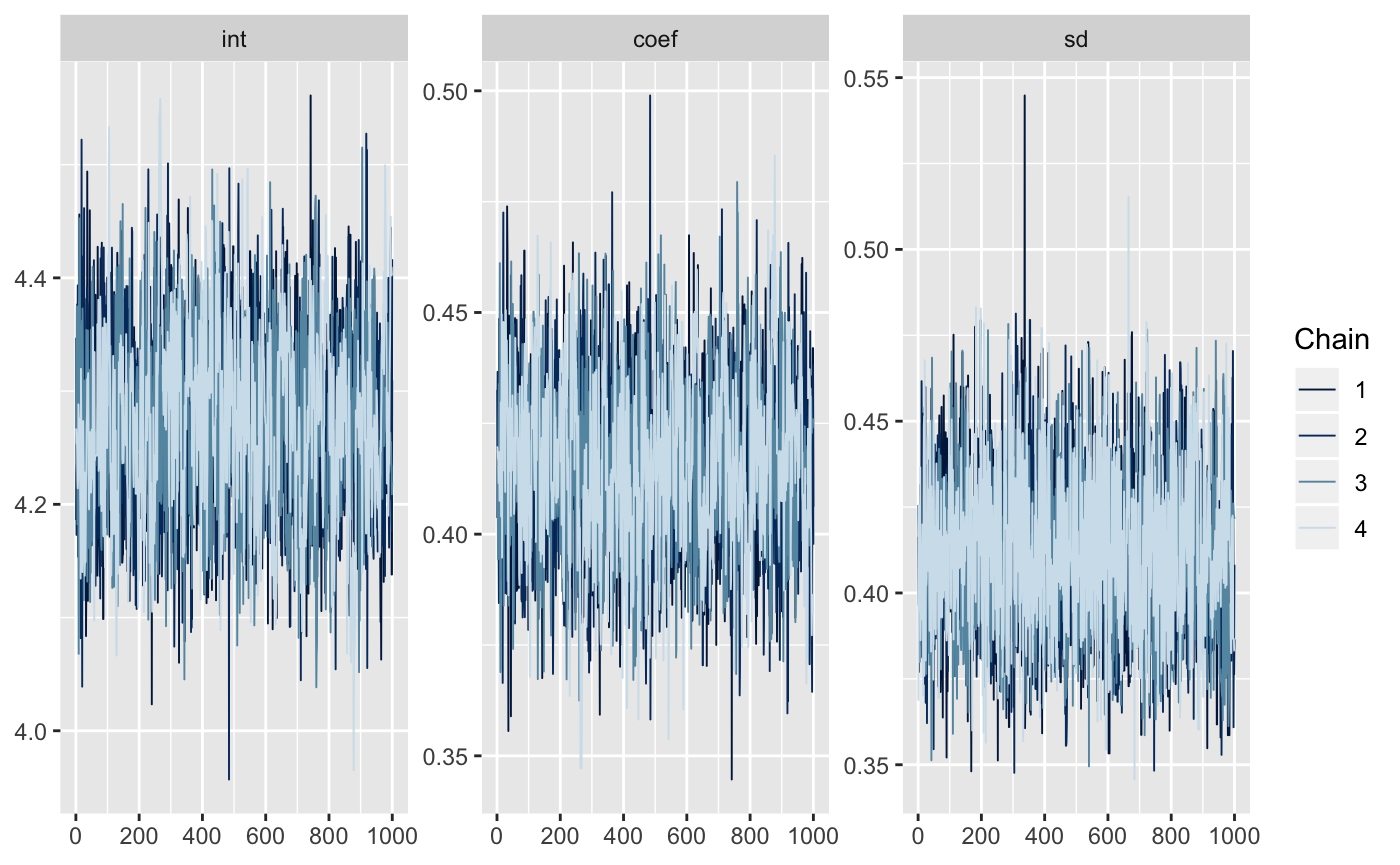
neat_draws <- mmcc::mcmc_to_dt(draws)

neat_draws
#>        iteration chain parameter     value
#>     1:         1     1       int 4.1861038
#>     2:         2     1       int 4.2272530
#>     3:         3     1       int 4.2348452
#>     4:         4     1       int 4.2048440
#>     5:         5     1       int 4.3188853
#>    ---                                    
#> 11996:       996     4        sd 0.3866304
#> 11997:       997     4        sd 0.3866304
#> 11998:       998     4        sd 0.3866304
#> 11999:       999     4        sd 0.3831778
#> 12000:      1000     4        sd 0.3831778

library(ggplot2)

ggplot(neat_draws[parameter == "int"],
       aes(x = iteration,
           y = value,
           colour = chain)) + 
    geom_line()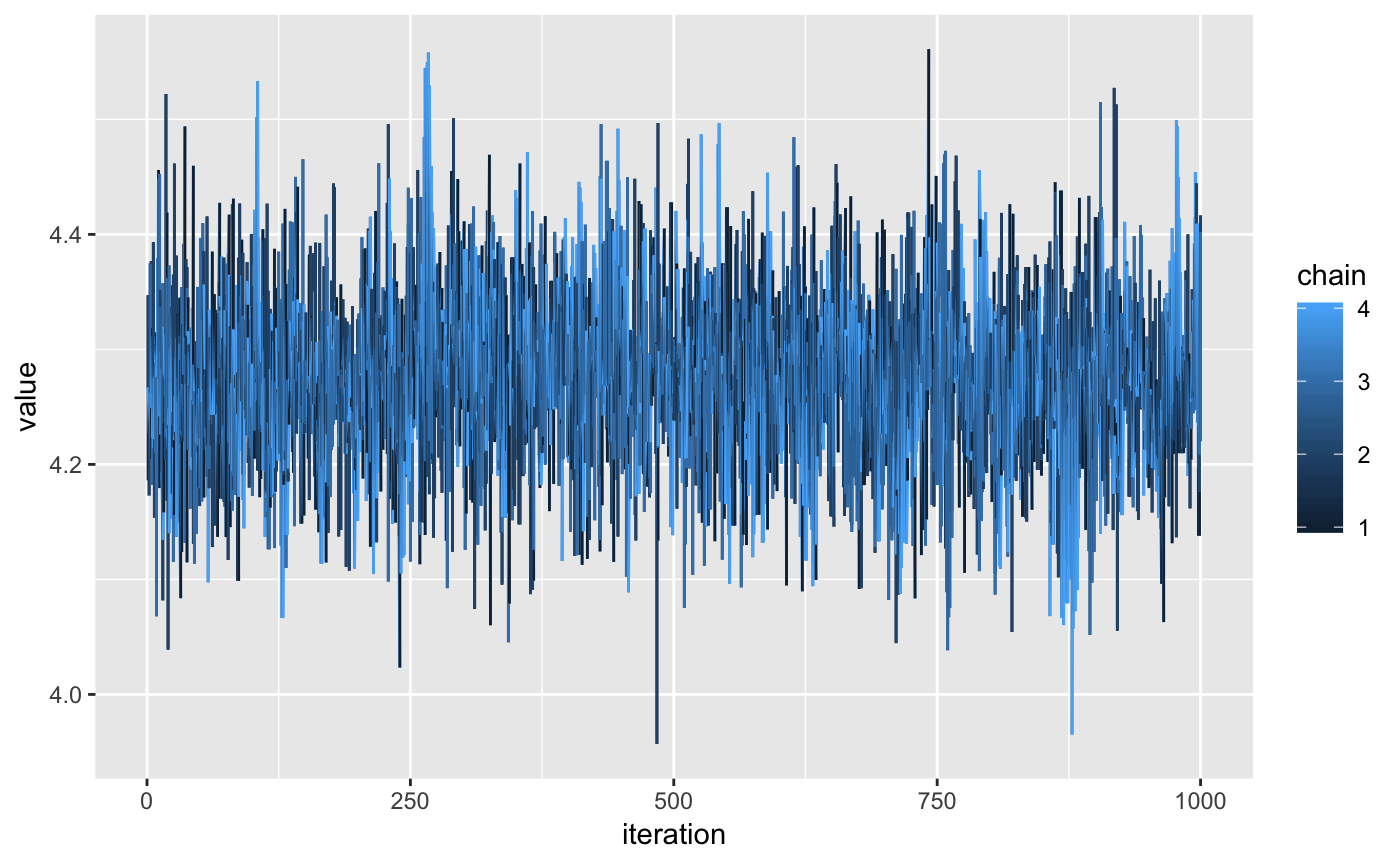

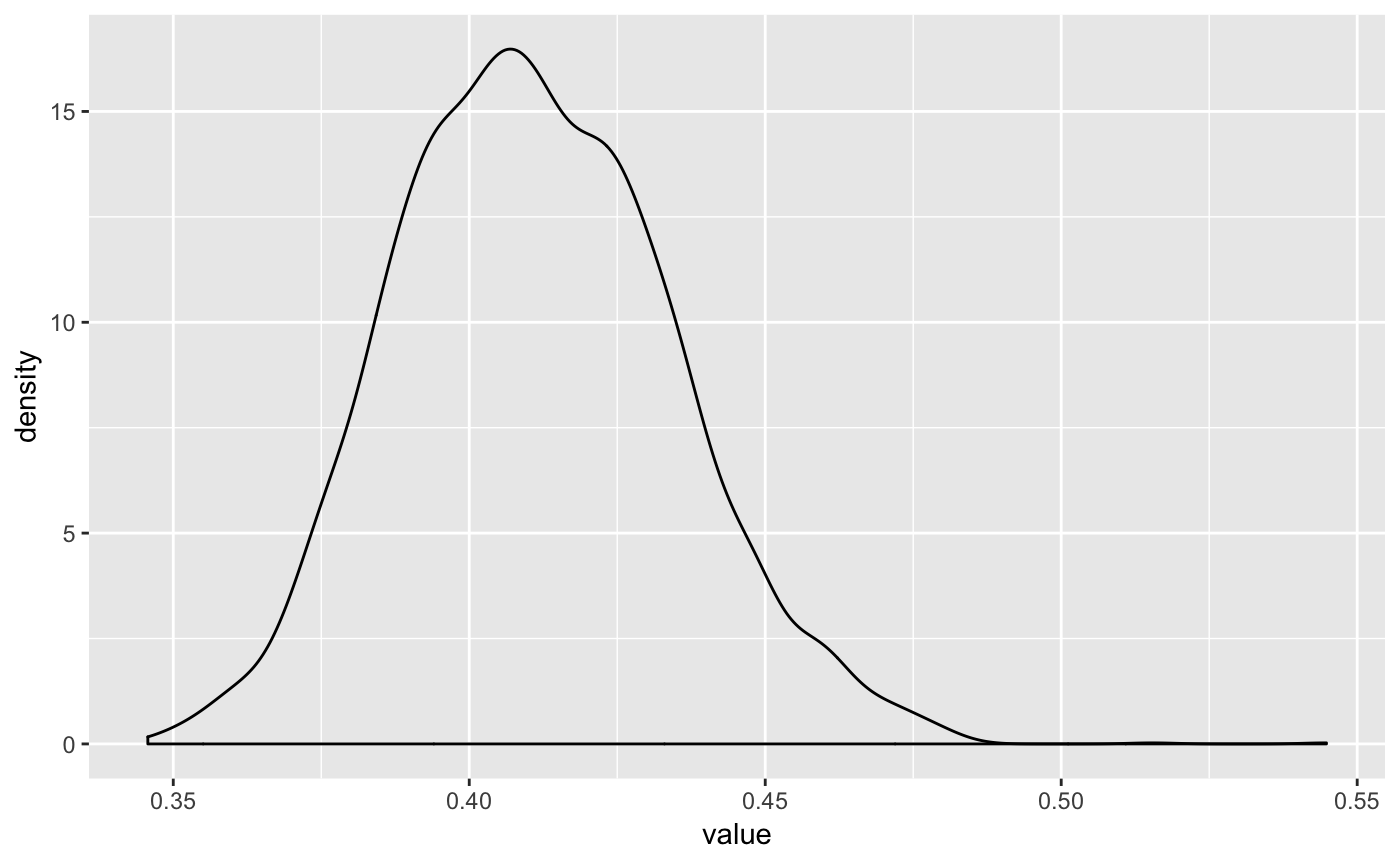
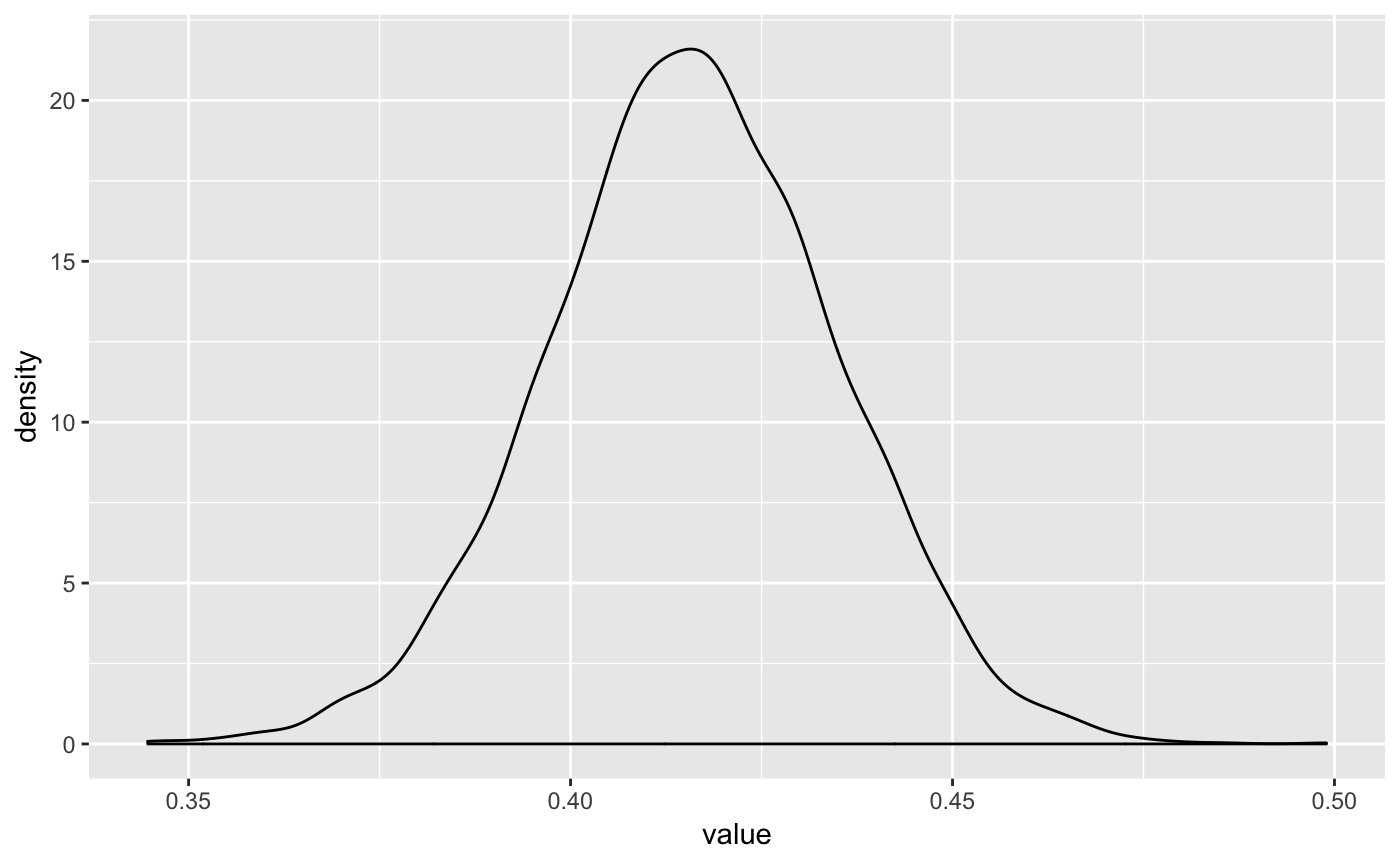
ggplot(neat_draws[parameter == "sd"],
       aes(x = value,
           colour = chain)) + 
    geom_density()

ggplot(neat_draws[parameter == "coef"],
       aes(x = value,
               colour = chain)) + 
    geom_density()

Or we can use some examples from bayesplot:

bayesplot::mcmc_hist(draws)
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

bayesplot::mcmc_dens(draws)

bayesplot::mcmc_trace(draws)